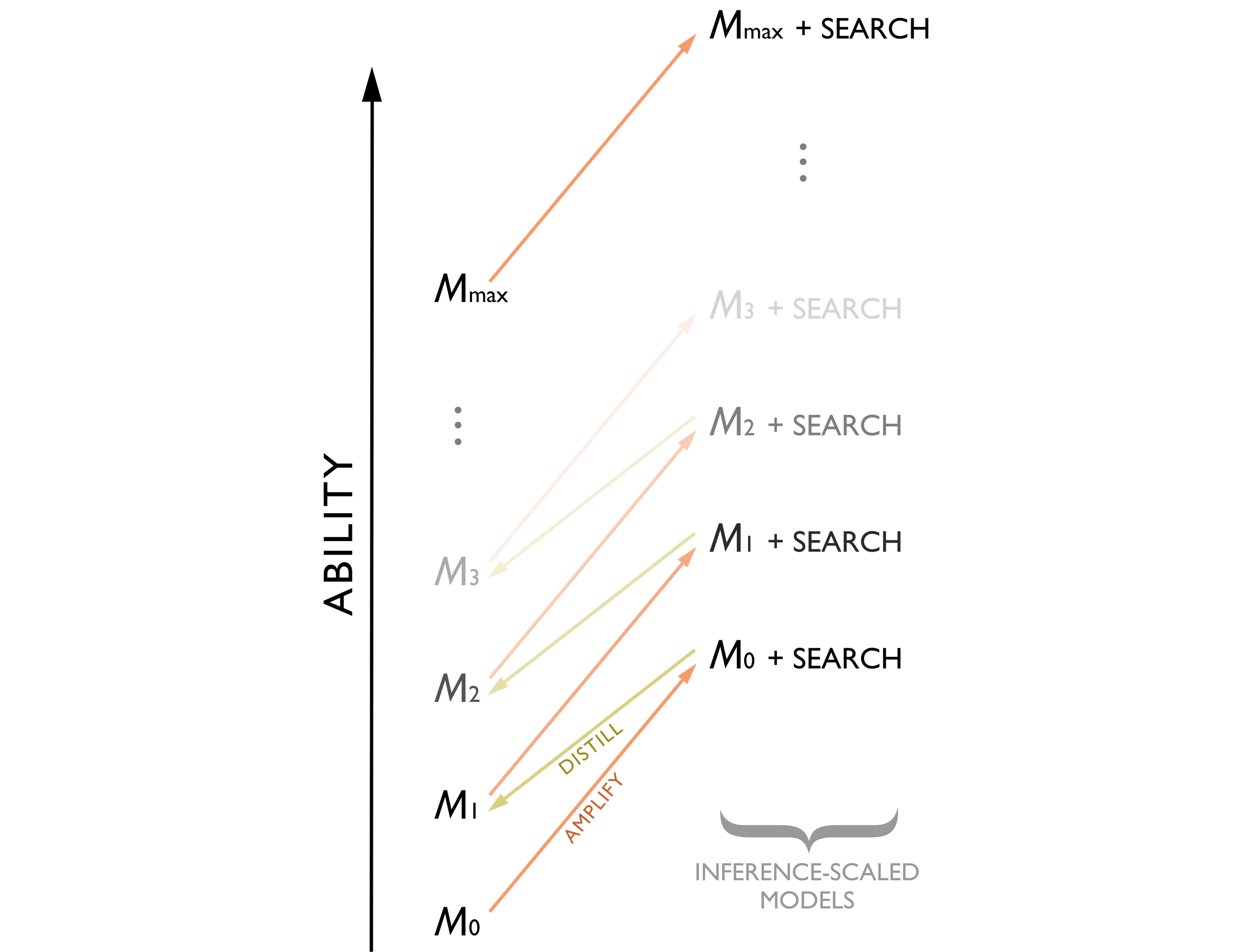Inference Scaling Reshapes AI Governance

The shift from scaling up the pre-training compute of AI systems to scaling up their inference compute may have profound effects on AI governance. The nature of these effects depends crucially on whether this new inference compute will primarily be used during external deployment or as part of a more complex training programme within the lab. Rapid scaling of inference-at-deployment would: lower the importance of open-weight models (and of securing the weights of closed models), reduce the impact of the first human-level models, change the business model for frontier AI, reduce the need for power-intense data centres, and derail the current paradigm of AI governance via training compute thresholds. Rapid scaling of inference-during-training would have more ambiguous effects that range from a revitalisation of pre-training scaling to a form of recursive self-improvement via iterated distillation and amplification.

The end of an era — for both training and governance

The intense year-on-year scaling up of AI training runs has been one of the most dramatic and stable markers of the Large Language Model era. Indeed it had been widely taken to be a permanent fixture of the AI landscape and the basis of many approaches to AI governance.

But recent reports from unnamed employees at the leading labs suggest that their attempts to scale up pre-training substantially beyond the size of GPT-4 have led to only modest gains which are insufficient to justify continuing such scaling and perhaps even insufficient to warrant public deployment of those models. A possible reason is that they are running out of high-quality training data. While the scaling laws might still be operating (given sufficient compute and data, the models would keep improving), the ability to harness them through rapid scaling of pre-training may not. What was taken to be a fixture may instead have been just one important era in the history of AI development; an era which is now coming to a close.

Just before the reports of difficulties scaling pre-training, OpenAI announced their breakthrough reasoning model, o1. Their announcement came with a chart showing how its performance on a difficult mathematics benchmark could be increased via scaling compute dedicated to post-training reinforcement learning (to improve the overall performance of the model); or by scaling the inference compute used on the current task.

This has led to intense speculation that the previous era of scaling pre-training compute could be followed by an era of scaling up inference-compute. In this essay, I explore the implications of this possibility for AI governance.

In some ways a move to scaling of inference compute may be a continuation of the previous paradigm (as lab leaders have been suggesting$^1$). For example, work on the trade-off between pre-training compute and inference compute suggests that (on the current margins) increasing inference compute on the task at hand by 1 order of magnitude often improves performance as much as increasing pre-training compute by 0.5 to 1 orders of magnitude. So we may be tempted to see it simply as an implementation detail in the bigger story of scaling up compute in general.

But a closer look suggests that may be a mistake. There are a number of key differences between scaling pre-training and scaling inference — both for the labs and for AI governance.

I shall argue that many ideas in AI governance will need either an adjustment or an overhaul. Those of us in the field need to look back at the long list of ideas we work with and see how this affects each one.

There is a lot of uncertainty about what is changing and what will come next.

One question is the rate at which pre-training will continue to scale. It may be that pre-training has topped out at a GPT-4 scale model, or it may continue increasing, but at a slower rate than before. Epoch AI suggests the compute used in LLM pre-training has been growing at about 5x per year from 2020 to 2024. It seems like that rate has now fallen, but it is not yet clear if it has gone to zero (with AI progress coming from things other than pre-training compute) or to some fraction of its previous rate.

A second — and ultimately more important — question concerns the nature of inference-scaling. We can view the current AI pipeline as pre-training (such as via next-token prediction), followed by post-training (such as RLHF or RLAIF), followed by deploying the trained model on a vast number of different tasks (such as through a chat interface or API calls).

The second question is whether the scaled-up inference compute will primarily be spent during deployment (like in o1 and R1) or as part of a larger and more complex post-training process (like the suggestions that OpenAI may have used trained o3 via many runs of o1). Each of these possibilities has important — but different — implications for AI governance.

Scaling inference-at-deployment

Let’s first consider the scenario where for the coming years, the lion’s share of compute scaling goes into scaling up the inference compute used at deployment. In this scenario, the pre-trained system is either stuck at GPT-4 level or only slowly progressing beyond that, while new capabilities are being rapidly unlocked via more and more inference compute. Some of this may be being spent in post-training as the system learns how to productively reason for longer times (e.g. the reinforcement learning in the left-hand chart of OpenAI’s o1 announcement), but for this scenario, we are supposing that this one-off cost is comparatively small and that the main thing being scaled is the deployment compute.

In this scenario, we may be able to use rules of thumb such as

Effective orders of magnitude = OOMs of pre-training + 0.7 × OOMs of inference

to estimate the capabilities of an inference-scaled model in terms of the familiar yardstick of pure pre-training. But overreliance on such formulas could obscure key changes in the new scaling paradigm — changes that stem from the way the benefits of inference-at-deployment depend upon the task at hand, the way the amount of inference can be tuned to the task, and the way the costs shift from training time to deployment time.  

Reducing the number of simultaneously served copies of each new model

It currently takes a vast number of chips to train a frontier model. Once the model is trained, those chips can be used for inference to deploy a large number of simultaneous copies of that model. Dario Amodei of Anthropic estimates this to be ‘millions’ of copies. This number of copies is a key parameter for AI governance as it affects the size of the immediate impact on the world the day the new model is ready. A shift to scaling inference-at-deployment would lower this number. e.g. if inference-at-deployment is scaled by two orders of magnitude, then this key parameter goes down by a factor of 100, and the new model can only be immediately deployed in 1% as many tasks as it would be if it had been scaled by pre-training compute.$^2$

Increasing the price of first human-level AGI systems

A related parameter is how expensive the first ‘human-level’ AI systems will be to run. By previous scaling trends we might expect the first such systems to cost much less than human labour, meaning that they could be immediately deployed at a great profit, which could be ploughed back into renting chips to run more copies of them in an escalating feedback loop. But each additional order of magnitude that goes to inference-at-deployment may increase the cost of using these systems by up to an order of magnitude.

This will blunt the immediate impact of reaching this threshold and may even be enough such that there is an initial period where we first have access to ‘human-level’ AGI systems at more than the cost of equivalent human labour. If so, such systems could be available to study (for safety work) or demonstrate (before the world’s leaders) before they have transformative effects on society.

Obviously the fact that AI is already much better than humans at some tasks while much worse at others complicates this idea of reaching ‘human-level’, but I believe it is still a useful lens. For example, you can ask whether the first systems that can perform a particular job better than humans will cost more or less than human wages for that job.

Reducing the value of securing model weights

Suppose that for frontier models, training compute plateaus at something like the GPT-4 level while inference-at-deployment scales by a factor of 100. Then the value of stealing model weights hasn’t increased over time — it is just the value of not having to train a GPT-4 level model (which has been decreasing over time by about 4x per year due to algorithmic efficiency improvements and Moore’s law). And even if the weights were stolen, the thief would still have to pay the high inference-at-deployment costs. If they intend to use the model at anything like the scale current leading models are used, these would be the lion’s share of the total costs and much higher than the training costs of the model they stole.

Reducing the benefits and risks of open-weight models

This also affects both the benefits and drawbacks of open-weight models. If open-weight models require vast amounts of inference-at-deployment from their users, then they are much less attractive to those users than models of equivalent capability that were entirely pre-trained (since then the model trainer has paid those costs for you). So open-weight models could become much less valuable for their users and also less dangerous in terms of proliferation of dangerous capabilities. They would become less strategically important overall.

Unequal performance for different tasks and for different users

Scaling inference-at-deployment helps with some kinds of tasks much more than others. It helps most with tasks where the solution is objectively verifiable, such as certain kinds of maths and programming tasks. It can also be useful for tasks involving many steps. Two good heuristics for the tasks that benefit from inference scaling are:

1. tasks that benefit from System 2–type thinking (methodical reasoning) when performed by humans,

2. tasks that typically take humans a long time (as this shows these tasks can benefit from a lot of thinking before diminishing marginal returns kick in).

Because some tasks benefit more from additional inference than others, it is possible to tailor the amount of inference compute to the task, spending 1,000x the normal amount for a hard, deep maths problem, while just spending 1x on problems that are more intuitive. This kind of tailoring isn’t possible with pre-training scaling, where scaling up by 10x increases the costs for everything.

A related change is that users with more money will likely be able to convert that into better answers. We’ve already seen this start to happen at OpenAI (the first frontier company to allow access to a model that scales inference-at-deployment). They now charge 10x as much for access to the version using the most inference-compute. We’d become accustomed to a dollar a day getting everyone the same quality of AI assistance. It was as Andy Warhol said about Coca Cola:

‘What’s great about this country is that America started the tradition where the richest consumers buy essentially the same things as the poorest. … the President drinks Coca Cola, Liz Taylor drinks Coca Cola, and just think, you can drink Coca Cola, too. A coke is a coke and no amount of money can get you a better coke than the one the bum on the corner is drinking.’

But scaling inference-at-deployment ends that.

Changing the business model and industry structure

The LLM business model has had a lot in common with software: big upfront development costs and then comparatively low marginal costs per additional customer. Having a marginal cost per extra user that is lower than the average cost per user encourages economies of scale where each company is incentivised to set low prices to acquire a lot of customers, which in turn tends to create an industry with only a handful of players. But if the next two orders of magnitude of compute scale-up go into inference-at-deployment instead of into pre-training, then this would change, upsetting the existing business model and perhaps allowing more room for smaller players in the industry.

Reducing the need for monolithic data centres

While training compute benefits greatly from being localised in the same data centre, inference-at-deployment can be much more easily spread between different locations. Thus if inference-at-deployment is being scaled by several orders of magnitude, it could avoid current bottlenecks concerning single large data centres, such as the need for a large amount of electrical power draw in a single place (which has started to require its own large powerplant). So if one hoped for the government to be able to exert some control over AI labs via the carrot of accelerated power plant approvals, inference-at-deployment may change that. And it will make it harder for governments to keep track of all the frontier models being trained by tracking the largest datacentres.

Breaking the strategy of AI governance via compute thresholds

Many AI governance frameworks are based around regulating only those models above a certain threshold of training compute. For example, the EU AI Act uses 10$^{25}$ FLOP while the US executive order uses 10$^{26}$ FLOP. This allows them to draw a line around the few potentially dangerous systems without needing to regulate the great majority of AI models. But if capabilities can be increased via scaling inference-at-deployment then a model whose training compute was below these thresholds might be amplified to become as powerful as those above them. For example, a model trained with 10$^{24}$ FLOP might have its inference scaled up by 4 OOM and perform at the level of a model trained with 10$^{27}$ FLOP. This threatens to break this entire approach of training-compute thresholds.

At first the threat might be that someone scales up inference-at-deployment by a very large factor for a small number of important tasks. If the inference scale-up is only happening on a small fraction of all tasks the model is deployed on, one could use a very high scale-up factor (such as 100,000x) and suddenly operate at the level of a new tier of model.

The main limitation on this at the moment is that many current techniques for inference scaling seem to hit plateaus that can’t be exceeded by any level of inference scale-up. Exceeding these plateaus requires substantial research time by AI scientists and engineers, such that if someone tried to use a GPT-4 level model with 100,000x the inference compute, it may not be able to make good use of most of that compute. However, labs are developing better ways to use large multipliers of inference compute before reaching performance plateaus and this work is proceeding very quickly. For example, OpenAI demonstrated their o3 model making use of 10,000x as much compute as their smallest reasoning model, o1-mini, and so presumably an even larger factor above their base model, GPT-4o.

Leading labs have also been scaling their data centres and improving algorithmic efficiency such that they may already have 100x the effective-compute of the first data centres capable of serving GPT-4 to customers. This would allow more than just a few people to use versions with greatly scaled-up inference-at-deployment. For example, OpenAI’s recently launched deep research model (based on o3) may well exceed the performance of a system pre-trained on 10$^{26}$ FLOP, even if it is technically below that threshold.

While one could try to change the governance threshold to incorporate the inference-at-deployment as well as the pre-training compute, this would face serious problems. The current framework aims to separate AI systems that could be dangerous from those that can’t be. It aims to regulate dangerous objects, not dangerous uses of objects. But a revised threshold would depend not just on the model but on how you are using it, which would be a different and more challenging kind of governance threshold.

Perhaps one way to save the compute thresholds is to say that they cover both systems above 10$^{26}$ FLOP of pre-training and systems above some smaller threshold (e.g. 10$^{24}$ FLOP of pre-training) that have had post-training to allow themselves to benefit from high inference-at-deployment. But this still suffers from increased complexity and fewer bright lines.

Overall, scaled up inference-at-deployment looks like a big challenge for governance via compute thresholds.

Scaling inference-during-training

AI labs may also be able to reap tremendous benefit from these inference-scaled models by using them as part of the training process. If so, the large scale-up of compute resources could go into post-training rather than deployment. This would have very different implications for AI governance.

In this section, we’ll focus on the implications of a pure strategy of using inference-scaling only during the training process. This will clarify what it contributes to the overall picture of AI governance, though realistically we will see inference-scaling in both training and deployment.

An obvious approach to scaling inference-during-training is to use an inference-scaled model to generate large amounts of high-quality synthetic data on which to pre-train a new base model. This would make sense if the challenges in scaling up pre-training beyond GPT-4 are due to running out of high-quality training data. For example, court documents  have revealed that Meta’s Llama3 team decided to train on an illegal Russian repository of copyrighted books, LibGen, because they were unable to reach GPT-4 level without it:

‘Libgen is essential to meet SOTA [state-of-the-art] numbers, across all categories, and it is known that OpenAI and Mistral are using the library for their models (through word of mouth).’

This strongly suggests that even though there are still many more unused tokens on the indexed web (about 30x as many as are used in GPT-4 level pre-training), performance is being limited by lack of high-quality tokens. There have already been attempts to supplement the training data with synthetic data (data produced by an LLM), but if the issue is more about quality than raw quantity, then they need the best synthetic data they can get.

Inference-scaling can help with this by boosting the capability of the model producing the synthetic data. One way to do this is via domains such as mathematics or programming where one can tell whether a generated solution is correct and how efficient it is. The training programme could involve generating lots of proofs and computer programs using advanced reasoning models until it finds high quality solutions, and then add those to the stock of data that goes into pre-training the next base model.

This access to ground truth in mathematical disciplines is particularly important for getting the right training signal. But even for domains that are less black and white, it may be possible to trade extra inference compute for better synthetic data. For example, one could generate many essays, run several rounds of editing on them, and then assess them for originality, importance of insight, and lack of detectable errors, putting only those of the highest quality into the stock of synthetic data.

Relatedly, one could apply this technique to the stock of human-generated training data, assessing each document in the training data and discarding those that are below-average in quality. This could either improve the average quality of the data they already use or make some fraction of the unused sources of data usable.

On its own, this approach of scaling inference-during-training to produce synthetic data for pre-training is not so interesting from an AI governance perspective. Its main direct effect is to allow the scaling of pre-training compute to recommence, breathing new life into the existing scaling paradigm.

But there is a modification of this approach that may have the potential to lead to explosive growth in capabilities. The idea is to rapidly improve a model’s abilities by amplifying its abilities (through inference scaling) then distilling those into a new model, and repeating this process many times. This idea is what powered the advanced self-play in DeepMind’s AlphaGo Zero, and was also independently discovered by Anthony et al. and, in the context of AI-safety, by Christiano.

In the case of AlphaGo Zero, you start with a base model, $M_0$, that takes a representation of the Go board and produces two outputs: a probability distribution over the available moves (representing the chance a skilled player would choose them) and a probability representing the chance the active player will eventually win the game.$^3$ This model will act as an intuitive ‘System 1’ approach to game playing, with no explicit search.

The training technique then plays 25,000 games of Go between two copies of $M_0$ amplified by a probabilistic technique for searching through the tree of moves and countermoves called Monte Carlo Tree Search (MCTS). That is, both players use MCTS with $M_0$ guiding the search by using its estimates of likely moves and position strength as a prior. By repeatedly calling $M_0$ in the search (thousands of times), we get a form of inference-scaling which amplifies the power of this model. We could think of it as taking the raw System 1 intuitions of the base model and embedding them in a System 2 reasoning process which thinks many moves ahead.

This amplified model is better than the base model at predicting the move most likely to win in each situation, but it is also much more costly. So we train a new model, $M_1$, to predict the outputs of $M_0$ + search. Following Christiano, I shall call this step distillation, though in the case of AlphaGo Zero, $M_1$ was simply $M_0$ with an additional stage of training. This trained its move predictions to be closer to the probability distribution over moves that $M_0$ + search gives and trained its board evaluations to be closer to the final outcome of the self-played games. While $M_1$ won’t be quite as good at Go as the amplified version of $M_0$, it is better than $M_0$ alone.

But why stop there? We can repeat this process, amplifying $M_1$ through inference-scaling by using it to guide the search process, producing a level of play beyond any seen so far ($M_1$ + search). This then gets distilled into a new model, $M_2$, and we proceed onwards and upwards, climbing higher and higher along the ladder of Go-playing performance.

After just 36 hours the best model (with search) had exceeded the ability of AlphaGo Lee (the version that beat world-champion Lee Sedol) which had been trained for months but lacked some innovations including this structure of iterated amplification and distillation. Within 72 hours AlphaGo Zero was able to defeat AlphaGo Lee by 100 games to zero. And after 40 days of training (and 29 million games of self-play$^4$) it reached its performance plateau, $M_{max}$, where the unamplified model could no longer meaningfully improve its predictions of the amplified model. At this point the amplified version had an estimated Elo rating of 5,185 — far beyond the 3,739 of AlphaGo Lee or the low 3,000s of the world’s best human players. Even when the final model was used without any search process (i.e. without any scaling of inference-at-deployment), it achieved a rating of 3,055 — roughly at the level of a human pro player despite playing from pure ‘intuition’ with no explicit reasoning.

It may be possible to use such a process of iterated distillation and amplification in the training of LLMs. The idea would be to take a model such as GPT-4o (which applied a vast amount of pre-training to provide it with a powerful System 1) and use it as the starting model, $M_0$.$^5$ Then amplify it via inference scaling into a model that uses a vast number of calls to $M_0$ to simulate System 2–type internal reasoning before returning its final answer (as o1 and R1 do). Then distill this amplified model into a new model, $M_1$, that is better able to produce the final answer from the amplified model without doing the hidden reasoning steps.$^6$ If this works, you now have model that is more capable than GPT-4o without using extra inference-at-deployment.

By iterating this process of amplification followed by distillation, it may be possible for the LLM (like AlphaGo Zero) to climb a very long way up this ladder before the process runs out of steam. And the time for each iteration may be substantially shorter than the time between major new pre-training runs. Like AlphaGo Zero, the final distilled model could display very advanced capabilities even without amplification. If this all worked, it would be a way of scaling inference-during-training to substantially quicken the rate of AI progress.

It is not at all clear whether this would work. It may plateau quickly, or require rapidly growing parameter counts to distill each new model, or take too long per step, or too many steps, or require years worth of engineering effort to overcome the inevitable obstacles that arise during the process.$^7$ But AlphaGo Zero does give us a proof of concept of a small team at a leading lab achieving take-off with such a process and riding its rapid ascent to reach capabilities far beyond the former state-of-the-art.

So iterated distillation and amplification provides a plausible pathway for scaling inference-during-training to rapidly create much more powerful AI systems. Arguably this would constitute a form of ‘recursive self-improvement’ where AI systems are applied to the task of improving their own capabilities, leading to a rapid escalation. While there have been earlier examples of this, they have often been on narrow domains (e.g. the game of Go) or have only applied to certain cognitive abilities (e.g. ‘learning how to learn’) and so been bottlenecked on other abilities. Iterated distillation and amplification of LLMs is a version that could credibly learn to improve its own general intelligence.

What does this mean for AI governance? A key implication is that scaling inference-during-training may mean we have less transparency into the best current models. While this use of inference inside the training process would reach the EU AI Act’s compute threshold, that threshold only requires oversight when the model is deployed.$^8$ Thus it may be possible for companies to substantially scale up the intelligence of their leading models without anyone outside knowing. AI governance may then have to proceed from a state of greater uncertainty about the state of the art. Relatedly, the lack of transparency would mean the public and policymakers wouldn’t be able to try these state-of-the-art models and so the overton window of available policy responses won’t be able to shift in response to them. This would lead to less regulation and a more abrupt shock to the world when the models at the top of the training ladder are deployed.

But perhaps most importantly, the possibility of training general models via iterated distillation and amplification could shorten the timelines until AGI systems with transformative impacts on the world. If this was combined with a lack of transparency about state of the art models during internal scaling, we couldn’t know for sure if timelines were shortening or not, making it hard to know whether emergency measures were required. All of this suggests that policies to require disclosure of current capabilities (and immediate plans for greater capabilities) would be very valuable.

Conclusions

The shift from scaling pre-training compute to scaling inference compute may have substantial implications for AI governance.

On the one hand, if much of the remaining scaling comes from scaling inference at deployment, this could have implications including:

• Reducing the number of simultaneously served copies of each new model

• Increasing the price of first human-level AGI systems

• Reducing the value of securing model weights

• Reducing the benefits and risks of open-weight models

• Unequal performance for different tasks and for different users

• Changing the business model and industry structure

• Reducing the need for monolithic data centres

• Breaking the strategy of AI governance via compute thresholds

On the other hand, if companies instead focus on scaling up the inference-during-training, then they may be able to use reasoning systems to create the high-quality training data needed to allow pre-training to continue. Or they may even be able to iterate this in the manner of AlphaGo Zero and scale faster than ever before — up the ladder of iterated distillation and amplification. This possibility may lead to:

• Less transparency into the state of the art models

• Less preparedness among the public and policymakers

• Shorter timelines to transformative AGI

Either way, the shift to inference-scaling also makes the future of AI less predictable than it was during the era of pre-training scaling. Now there is more uncertainty about how quickly capabilities will improve and which longstanding features of the frontier AI landscape will still be there in the new era. This uncertainty will make planning for the next few years more difficult for the frontier labs, for their investors, and for policymakers. And it may provide a premium on agility: on the ability to first spot what is happening and pivot in response.

All of this analysis should be taken just as a starting point for the effects of inference-scaling on AI governance. As this transition continues it will be important for the field to track the which types of inference-scaling are happening and thus better understand which of these issues we are facing.

Appendix. Comparing the costs of scaling pre-training vs inference-at-deployment

Scaling up pre-training by an order of magnitude and scaling up inference-at-deployment by an order of magnitude may have similar effects on the capabilities of a model, but they can have quite different effects on the total compute cost of the project. Which one is more expensive depends on the circumstances in a rather complex way.

Let’s focus on the total amount of compute used for an AI system over its lifetime as the cost of that system (though this is not the only thing one might care about). The total amount of compute used for an AI system is equal to the amount used in training plus the amount used in deployment:

$C = C_{pre-training} + C_{post-training} + C_{deployment}$

Let $N$ be the number of parameters in the model, $D$ be the number of data tokens it is trained on, $d$ be the number of times the model is deployed (e.g. the number of questions it is asked) and $I$ be the number of inference steps each time it is deployed (e.g. the number of tokens per answer). Then this approximately works out to:$^9$

$C  \approx  ND  +  C_{post-training}  +  dNI$

Note that scaling up the number of parameters, $N$, increases both pre-training compute and inference compute, because you need to use those parameters each time you run a forward pass in your model. But scaling up $D$ doesn’t directly affect deployment costs. Some typical rough numbers for these variables in GPT-4 level LLMs are:

N = 10$^{12}$           D = 10$^{13}$           I = 10$^{3}$              d = ?

On this rough arithmetic, the deployment costs overtake the pre-training costs when the total number of tokens generated in deployment ($dI$) is greater than the total number of training tokens $D$. That would require $d$ > 10$^{10}$. Apparently, this is usually the case, with deployment compute exceeding total training compute on commercial frontier systems.$^{10}$

The most standard way of training LLMs to minimise training compute involves scaling up $N$ and $D$ by the same factor. For example, if you scale up training compute by 1 OOM, that means 0.5 OOMs more parameters and 0.5 OOMs more data. So scaling up training compute by 1 OOM also increases deployment compute by 0.5 OOM. In contrast, scaling up inference-at-deployment by an order of magnitude doesn’t (directly) affect pre-training compute.

When either the pre-training compute ($ND$) or the deployment compute ($dNI$) is the bulk of the total (including $C_{post-training}$), there are some simple approximations for the costs of scaling. If $C_{pre-training} \gg C_{post-training} + C_{deployment}$, then scaling pre-training by 10x increases costs by nearly 10x, while scaling inference-at-deployment ($I$) by 10x doesn’t affect the total much. Whereas if $C_{deployment} \gg C_{pre-training} + C_{post-training}$, then scaling pre-training by 10x increases costs by ~3x (from the larger number of parameters needed at deployment), while scaling inference-at-deployment by 10x increases costs by nearly 10x. So there is some incentive to balance these numbers where possible.

It is important to note that the costs of scaling inference-at-deployment depend heavily on how much deployment you are doing. If you just use the model to answer a single question, then you could scale it all the way until it generates as many tokens as you pretrained on (i.e. trillions) before it appreciably affects your overall compute budget. While if you are scaling up the inference used for every question, your overall compute budget could be affected even by a 2x scale up.

$^1$ e.g. Dario Amodei has said ‘Every once in a while, the underlying thing that is being scaled changes a bit, or a new type of scaling is added to the training process. From 2020-2023, the main thing being scaled was pretrained models: models trained on increasing amounts of internet text with a tiny bit of other training on top. In 2024, the idea of using reinforcement learning (RL) to train models to generate chains of thought has become a new focus of scaling.’

$^2$ Or, somewhat equivalently, it might be better thought of as slowing these systems down by that factor (e.g. 100x). Amodei’s estimate is that AI systems are currently 10x–100x human speed, but if they reach intelligence via inference scaling, they may be slower than humans. Both ways of looking at it lead to the same reduction in the ‘human-days-equivalent of AI work each day’ when the systems are switched from training to deployment.

$^3$ For AlphaGo Zero, the goal was to start with zero information about Go and learn everything, so $M_0$ was simply a randomly initialised network. But it is also possible to start with a more advanced network as $M_0$, such as one trained to imitate human behaviour.

$^4$ Given 29 million games of self-play and a set-up with 25,000 games before each distillation, there were presumably 1,160 iterations of amplification and distillation before it reached its plateau, such that $M_{max}$ is $M_{1160}$.

$^5$ Like o1 and R1, we would presumably include additional RL post-training to prepare it for use in inference scaling.

$^6$ Here $M_1$ could be a fresh model distilled from the inference-scaled $M_0$, or it could be $M_0$ with fine-tuning to make it behave more like the inference-scaled $M_0$.

$^7$ It is also possible that it will work in some domains (such as mathematics and coding) but not others, leading to superhuman capabilities in several new domains, but not across the board.

$^8$ And only when deployed inside the EU itself, where OpenAI’s inference-scaled model deep research is conspicuously absent.

$^9$ I’m simplifying some of the details (such as the precise coefficients for each term) to make the overall structure of the equation clearer.

$^{10}$ This has led to methods of training that use more training compute than is Chinchilla-optimal because the smaller model leads to compensating savings on the deployment compute

12 February 2025

The Scaling Paradox

AI capabilities have improved remarkably quickly, fuelled by the explosive scale-up of resources being used to train the leading models. But if you examine the scaling laws that inspired this rush, they actually show extremely poor returns to scale. What’s going on?

AI Scaling is Shockingly Impressive

The era of LLMs has seen remarkable improvements in AI capabilities over a very short time. This is often attributed to the AI scaling laws — statistical relationships which govern how AI capabilities improve with more parameters, compute, or data. Indeed AI thought-leaders such as Ilya Sutskever and Dario Amodei have said that the discovery of these laws led them to the current paradigm of rapid AI progress via a dizzying increase in the size of frontier systems.

Before the 2020s, most AI researchers were looking for architectural changes to push the frontiers of AI forwards. The idea that scale alone was sufficient to provide the entire range of faculties involved in intelligent thought was unfashionable and seen as simplistic.

A key reason it worked was the tremendous versatility of text. As Turing had noted more than 60 years earlier, almost any challenge that one could pose to an AI system can be posed in text. The single metric of human-like text production could therefore assess the AI’s intellectual competence across a huge range of domains. The next-token prediction scheme was also an instance of both sequence prediction and compression — two tasks that were long hypothesized to be what intelligence is fundamentally about.

By the time of GPT-3 it was clear that it was working. It wasn’t just a dry technical metric that was improving as the compute was scaled up — the text was qualitatively superior to GPT-2 and showed signs of capturing concepts that were beyond that smaller system.

Scaling has clearly worked, leading to very impressive gains in AI capabilities over the last five years. Many papers and AI labs trumpet the success of this scaling in their latest results and show graphs suggesting that the gains from scaling will continue.

For example, here is a chart from OpenAI’s release of their o1 model, captioned: ‘o1 performance smoothly improves with both train-time and test-time compute’.

AI Scaling is Shockingly Unimpressive

But let’s take a closer look at what that chart is showing us. On the y-axis, their measure of AI performance is the model’s accuracy on mathematics problems aimed at elite high school students (via the challenging AIME data set). But the x-axis, showing the amount of compute at training-time and test-time is on a log scale. So the nice straight lines are really showing very serious diminishing returns to more compute for their model.

Specifically, the model shows logarithmic returns to compute. We can put this in more familiar terms by flipping it around: increasing the accuracy of the model’s outputs requires exponentially more compute.

That is not generally a recipe for success. In computer science exponential resource usage for linear gains is typically considered to be a sign the problem is intractable, or at least is intractable to the approach you are using. Indeed, the requirement of exponential increases in resources in time or space to continue making progress is characteristic of a brute force approach. It is the relationship you often get with the most naive approaches — those that simply try every possible solution, one by one.

And o1 isn’t the only place we see this. There was a very perceptible leap from GPT-2 to GPT-3 and from GPT-3 to GPT-4. But each successive model used about 70 times as much compute as the one before (4e21 → 3e23 → 2e25 FLOP). In every other aspect of life we would certainly be hoping to see a perceptible improvement if we put 70 times as many resources into it. And normally we’d consider something that kept requiring such exponentially increasing inputs to see visible progress as proof that things were going badly; that the approach was not successfully scaling.

The recent progress in AI hasn’t been entirely driven by increased computational resources. Epoch AI’s estimates are that compute has risen by 4x per year, while algorithmic improvements have divided the compute needed by about 3 each year. This means that over time, the effective compute is growing by about 12x per year, with about 40% of this gain coming from algorithmic improvements.

But these algorithmic refinements aren’t improving the scaling behaviour of AI quality in terms of resources. If it required exponentially more compute to increase quality, it still does after a year of algorithmic progress, it is just that the constant out the front is a factor of 3 lower. In computer science, an algorithm that solves a problem in exponential time is not considered to be making great progress if researchers keep lowering the constant at the front.

What about the famed scaling laws for LLMs? Don’t they show that LLMs scale so well with resources that this scaling should be the cornerstone in leading labs’ strategies? Let’s look at the key graphs from OpenAI’s 2020 paper ‘Scaling Laws for Neural Language Models’:

These show a steady improvement in test loss (a measure of inaccuracy of the model) as compute, data, and parameters increase. It appears at first that the model’s inaccuracy is marching down to very low levels without diminishing returns. However that is deceptive. First, both x and y axes are logarithmic, so this is actually a power law relationship (which can involve diminishing returns). Second, because the axes have been automatically clipped and rescaled to make the graph start in one corner and end in the opposite corner, there is literally nothing you can tell from the shape or slope of these graphs beyond them being some kind of power law. (If you were to equalise scale on the x and y axes, the slope would become informative and you would instantly see that they are extremely shallow slopes — thus extremely inefficient scaling.)

But if you look at the numbers on the x axes (the resources used), you can see that they vary over orders of magnitude while in each case the y-axis only covers about half an order of magnitude. For example, on the first graph, lowering the test loss by a factor of 2 (from 6 to 3) requires increasing the compute by a factor of 1 million (from 10$^{–7}$ to 10$^{–1}$). This shows that the accuracy is extraordinarily insensitive to scaling up the resources used. Or put another way, there are extreme diminishing returns to increased resource input.

A useful way to view this is to understand the exponents on these power law relationships (the power that things are being raised to). Each graph contains an embedded formula showing that the loss is proportional to the resource raised to a very small negative number. It is negative because in this setting the quality of the system is measured with a scale where lower numbers (lower inaccuracies) are better. It will be easier to understand what is going on if we invert that. So let’s define a measure of accuracy as the reciprocal of the test loss. On this revised measure, what used to be halving inaccuracy is now called doubling accuracy.

Using this measure of accuracy, we can remove the negatives from those powers. We see that the first power is now 0.050. What this means is that accuracy scales with the amount of compute used as the 1/20th power. Many of us are not that familiar with fractional powers but may recall that the square root function is equivalent to the 1/2 power. So here accuracy is growing slower than the square root of the square root of the square root of the square root of the resources. That sounds slow, but it is still a bit hard to understand or compare.

Fortunately, we can make this much more intuitive if we flip it around and ask how quickly required resources increase as a function of desired accuracy. To get that, we just take the reciprocal of the powers listed in the paper. This tells us that the compute required scales as the 20th power of the desired accuracy. i.e. if $C$ is compute and $a$ is accuracy, then $C$ = $k_C$ $a^{20}$, for some constant $k_C$. This exponent of 20 is why halving the loss (from 6 to 3) in the first graph required the compute to be doubled 20 times (a factor of 1 million). Similarly for data, $D$ = $k_D$ $a^{11}$, and for number of parameters, $N$ = $k_N$ $a^{13}$. Exponents this high are so rare in statistical relationships that you’d be forgiven for thinking that they were footnote markers.

Here is a redrawn version of the first scaling law, showing the extremely steep increase in compute required for a given accuracy level:

So the required resources grow polynomially with the desired level of accuracy. This is better than the exponential growth in resources we considered before. In computer science, the boundary between what is tractable and intractable is often roughly drawn as that between where the required resources scale polynomially and where they scale exponentially. But that is partly because the powers seen on polynomials in computer science are rarely higher than 3. Something that scales as the 11th, 13th, or 20th power is a case where the resources required are absolutely blowing up as desired accuracy increases and a problem whose required resources scaled so poorly would rarely be considered tractable.

Does the more recent Chinchilla scaling law paper make things better? No, if anything it makes them worse. While it does not directly plot how loss scales with each resource type, it does plot it for compute (see the grey curve in the graph below).

This grey curve is clearly not quite a straight line on this log-log chart and thus not a power law. In this study, increased quality requires more resources than a power law would predict, so resources required grow faster than polynomially, meaning even worse scaling.

Reconciling These Views

So what is going on here? Is AI scaling extremely impressive or is it disappointingly poor? How can we reconcile these perspectives?

There isn’t a simple answer. It depends on what we’re assessing.

From a logistics standpoint, it is impressive how quickly leading labs have been able to scale up their data centres and training runs. Quadrupling the size of your infrastructure every year is an amazing logistical achievement. But from most people’s point of view, it should be taken as being on the costs side of the ledger rather than the benefits side.

If we set aside these dramatically increasing costs, progress in AI capabilities has been impressive over the era of rapid scaling, and a lot of this impressiveness is indeed due to the scaling. Most measures of AI capabilities don’t show exponential progress over time, but there is no doubt this has been a heady rate of progress for AI in qualitative terms, with a feeling that it is even quicker than the five years before, in which deep learning had already set a cracking pace.

In terms of AI progress per resource, or per dollar, things are probably getting worse on most measures. This is what the pessimism about scaling laws is getting at. Measures of quality are increasing far slower than the exponentially mounting costs.

So why were people like Ilya Sutskever and Dario Amodei so impressed by the scaling laws? The answer is that there was a lot of headroom in compute — a lot of room to scale those costs.  Even if the resources needed would be thousands of times larger than the largest ever ML experiment, they saw that this (1) was still within the feasible set of things a large company could fund and (2) would still be a good deal given the vast potential benefits.

For on the high end of possibilities, we are talking about something that could potentially replace more than half of all human labour in the world, and perhaps bring forward scientific and technological advances that human labour would have taken centuries to reach. In other words, while the costs could escalate wildly, a deep-pocketed project might reach benefits of extreme value before it ran out of money. And those benefits might be worth more than enough to justify those (very high) costs.

More prosaically, we can note that it is entirely possible that financial returns will scale very quickly as a function of the technical measures of AI quality. If so, then even though standard measures of AI quality scale poorly as a function of resources, the financial returns might still scale very well as a function of resources. Indeed, if they scale better than linearly, that would create a paradigm of increasing marginal returns which would explain a landscape with a small number of players, each investing as much as they possibly can.

If the financial benefits of the intermediate systems keep generating enough profit to pay for the next training run then one can ride this process up to the point where non-financial constraints (such as power use, energy use, chip fabrication, or running out of training data) prevent further scaling.

Furthermore, at a certain quality level the AI systems may be capable enough to improve themselves, searching for and implementing the kinds of algorithmic efficiencies and breakthroughs that human AI scientists seek today. If so, then continued scaling up of AI training runs over the rest of the decade may be enough to get AI systems to the bottom of this escalator, where they are smart enough to ride it up through some number of floors of recursive self-improvement before the process tops out at some higher level. The hope of reaching this new regime of self-improvement is another reason why leading labs may be excited to push through this quick — but extraordinarily inefficient — scaling process.

We can compress much of this down to the following observations:

• AI progress as a function of time is impressive even if AI progress as a function of resources is not.

• The scaling laws are impressively smooth and long-lasting, but are a proof of poor but predictable scaling, rather than impressive scaling.

• While we know that AI quality metrics scale very poorly with respect to resources, the real-world impacts may scale much better.

Finally, it is worth noting that the sheer inefficiency of how current AI systems scale may suggest that there are other approaches which scale substantially more efficiently. The human mind (which doesn’t require an entire internet of data to achieve general intelligence) shows this is possible. If so, we might someday see a step change in AI capabilities when someone discovers a learning architecture that delivers much stronger returns to scale then turns the full force of the industry’s exponentially scaled data centres upon it.

13 January 2025

On the Value of Advancing Progress

(PDF available)

I show how a standard argument for advancing progress is extremely sensitive to how humanity’s story eventually ends. Whether advancing progress is ultimately good or bad depends crucially on whether it also advances the end of humanity. Because we know so little about the answer to this crucial question, the case for advancing progress is undermined. I suggest we must either overcome this objection through improving our understanding of these connections between progress and human extinction or switch our focus to advancing certain kinds of progress relative to others — changing where we are going, rather than just how soon we get there.$^1$

Things are getting better. While there are substantial ups and downs, long-term progress in science, technology, and values have tended to make people’s lives longer, freer, and more prosperous. We could represent this as a graph of quality of life over time, giving a curve that generally trends upwards.

What would happen if we were to advance all kinds of progress by a year? Imagine a burst of faster progress, where after a short period, all forms of progress end up a year ahead of where they would have been. We might think of the future trajectory of quality of life as being primarily driven by science, technology, the economy, population, culture, societal norms, moral norms, and so forth. We’re considering what would happen if we could move all of these features a year ahead of where they would have been.

While the burst of faster progress may be temporary, we should expect its effect of getting a year ahead to endure.$^2$ If we’d only advanced some domains of progress, we might expect further progress in those areas to be held back by the domains that didn’t advance — but here we’re imagining moving the entire internal clock of civilisation forward a year.

If we were to advance progress in this way, we’d be shifting the curve of quality of life a year to the left. Since the curve is generally increasing, this would mean the new trajectory of our future is generally higher than the old one. So the value of advancing progress isn’t just a matter of impatience — wanting to get to the good bits sooner — but of overall improvement in people’s quality of life across the future.

Figure 1. Sooner is better. The solid green curve is the default trajectory of quality of life over time, while the dashed curve is the trajectory if progress were uniformly advanced by one year (shifting the default curve to the left). Because the trajectories trend upwards, quality of life is generally higher under the advanced curve. To help see this, I’ve shaded the improvements to quality of life green and the worsenings red.

That’s a standard story within economics: progress in science, technology, and values has been making the world a better place, so a burst of faster progress that brought this all forward by a year would provide a lasting benefit for humanity.

But this story is missing a crucial piece.

The trajectory of humanity’s future is not literally infinite. One day it will come to an end. This might be a global civilisation dying of old age, lumbering under the weight of accumulated bureaucracy or decadence. It might be a civilisation running out of resources: either using them up prematurely or enduring until the sun itself burns out. It might be a civilisation that ends in sudden catastrophe — a natural calamity or one of its own making.

If the trajectory must come to an end, what happens to the previous story of an advancement in progress being a permanent uplifting of the quality of life? The answer depends on the nature of the end time. There are two very natural possibilities.

One is that the end time is fixed. It is a particular calendar date when humanity would come to an end, which would be unchanged if we advanced progress. Economists would call this an exogenous end time. On this model, the standard story still works — what you are effectively doing when you advance progress by a year is skipping a year at current quality of life and getting an extra year at the final quality of life, which could be much higher.

Figure 2. Exogenous end time. Advancing progress with an unchanging end time. Note that the diagram is not to scale (our future is hopefully much longer).

The other natural model is that when advancing progress, the end time is also brought forward by a year (call it an endogenous end time). A simple example would be if there were a powerful technology which once discovered, inevitably led to human extinction shortly thereafter — perhaps something like nuclear weapons, but more accessible and even more destructive. If so, then advancing progress would bring forward this final invention and our own extinction.

Figure 3. Endogenous end time. Advancing progress also brings forward the end time.

On this model, there is a final year which is much worse under the trajectory where progress is advanced by a year. Whether we assume the curve suddenly drops to zero at the end, or whether it declines more smoothly, there is a time where the upwards march of quality-of-life peaks and then goes down. And bringing the trajectory forward by a year makes the period after the peak worse, rather than better. So we have a good effect of improving the quality of life for many years combined with a bad effect of bringing our demise a year sooner.

It turns out that on this endogenous model, the bad effect always outweighs the good: producing lower total and average quality of life for the period from now until the original end time. This is because the region under the advanced curve is just a shifted version of the same shape as the region under the default curve — except that it is missing the first slice of value that would have occurred in the first year.$^3$ Here advancing progress involves skipping a year at the current quality of life and never replacing it with anything else. It is like skipping a good early track on an album whose quality steadily improves — you get to the great stuff sooner, but ultimately just hear the same music minus one good song.

So when we take account of the fact that this trajectory of humanity is not infinite, we find that the value of uniformly advancing progress is extremely sensitive to whether the end of humanity is driven by an external clock or an internal one.

Both possibilities are very plausible. Consider the ways our trajectory might play out that we listed earlier. We can categorise these by whether the end point is exogenous or endogenous.

Exogenous end points:

• enduring until some external end like the sun burning out

• a natural catastrophe like a supervolcanic eruption or asteroid impact

Endogenous end points:

• accumulation of bad features like bureaucracy or decadence

• prematurely running out of resources

• anthropogenic catastrophe such as nuclear war

Whether advancing all kinds of progress by a short period of time is good or bad, is thus extremely sensitive to whether humanity’s ultimate end is caused by something on the first list or the second. If we knew that our end was driven by something on the second list, then advancing all progress would be a bad thing.

⁂

I am not going to attempt to adjudicate which kind of ending is more likely or whether uniformly advancing progress is good or bad. Importantly — and I want to be clear about this — I am not arguing that advancing progress is a bad thing.

Instead, the point is that whether advancing progress is good or bad depends crucially on an issue that is rarely even mentioned in discussions on the value of progress. Historians of progress have built a detailed case that (on average) progress has greatly improved people’s quality of life. But all this rigorous historical research does not bear on the question of whether it will also eventually bring forward our end. All the historical data could thus be entirely moot if it turns out that advancing progress has also silently shortened our future lifespan.

One upshot of this is that questions about what will ultimately cause human extinction$^4$ — which are normally seen as extremely esoteric — are in fact central to determining whether uniform advancements of progress are good or bad. These questions would thus need to appear explicitly in economics and social science papers and books about the value of progress. While we cannot hope to know about our future extinction with certainty, there is substantial room for clarifying the key questions, modelling how they affect the value of progress, and showing which parameter values would be required for advancing all progress to be a good thing.

Examples of such clarification and modelling would include:

• Considerations of the amount of value at stake in each case.$^5$

• Modelling existential risk over time, such as with a time-varying hazard rate.$^6$

• Allowing the end time (or hazard curve) to be neither purely exogenous nor purely endogenous.$^7$

Note that my point here isn’t the increasingly well-known debate about whether work aimed at preventing existential risks could be even more important than work aimed at advancing progress.$^8$ It is that considerations about existential risk undermine a promising argument for advancing progress and call into question whether advancing progress is good at all.

Why hasn’t this been noticed before? The issue is usually hidden behind a modelling assumption of progress continuing over an infinite future. In this never-ending model, when you pull this curve sideways, there is always more curve revealed. It is only when you say that it is of a finite (if unknown) length that the question of what happens when we run out of curve arises. There is something about this that I find troublingly reminiscent of a Ponzi scheme: in the never-ending model, advancing progress keeps bringing forward the benefits we would have had in year t+1 to pay the people in year t, with the resulting debt being passed infinitely far into the future and so never coming due.

Furthermore, the realisation that humanity won’t last for ever is surprisingly recent — especially the possibility that its lifespan might depend on our actions.$^9$ And the ability to broach this in academic papers without substantial pushback is even more recent. So perhaps it shouldn’t be surprising that this was only noticed now.

The issue raised by this paper has also been masked in many economic analyses by an assumption of pure time-preference: that society should have a discount rate on value itself. If we use that assumption, we end up with a somewhat different argument for advancing progress — one based on impatience; on merely getting to the good stuff sooner, even if that means getting less of it.

Even then, the considerations I’ve raised would undermine this argument. For if it does turn out that advancing progress across the board is bad from a patient perspective, then we’d be left with an argument that ‘advancing progress is good, but only due to fundamental societal impatience and the way it neglects future losses’. The rationale for advancing progress would be fundamentally about robbing tomorrow to pay for today, in a way that is justified only because society doesn’t (or shouldn’t) care much about the people at the end of the chain when the debt comes due. This strikes me as a very troubling position and far from the full-throated endorsement of progress that its advocates seek.

Could attempts to advance progress have some other kind of predictable effect on the shape of the curve of quality of life over time?$^{10}$ They might. For instance, they might be able to lengthen our future by bringing forward the moment we develop technologies to protect us from natural threats to our survival. This is an intriguing idea, but there are challenges to getting it to work: especially since there isn’t actually much natural extinction risk for progress to reduce, whereas progress appears to be introducing larger anthropogenic risks.$^{11}$ Even if the case could be made, it would be a different case to the one we started with — it would be a case based on progress increasing the duration of lived experience rather than its quality. I’d be delighted if such a revised case can be made, but we can’t just assume it.$^{12}$

If we were to advance some kinds of progress relative to others, we could certainly make large changes to the shape of the curve, or to how long humanity lasts.$^{13}$ But this is not even a different kind of argument for the value of progress; it is a different kind of intervention, which we could call differential progress.$^{14}$ This would not be an argument that progress is generally good, but that certain parts of it are. Again, I’m open to this argument, but it is not the argument for progress writ large that its proponents desire.

And it may have some uncomfortable consequences. If advancing all progress would turn out to be bad, but advancing some parts of it would be good, then it is likely that advancing the remaining parts would be even more bad. Since some kinds of progress are more plausibly linked to bringing about an earlier demise (e.g. nuclear weapons, climate change, and large-scale resource depletion only became possible because of technological, economic, and scientific progress) these parts may not fare so well in such an analysis. So it may really be an argument for differentially boosting other kinds of progress, such as moral progress or institutional progress, and perhaps even for delaying technological, economic, and scientific progress.

It is important to stress that through all of this we’ve only been exploring the case for advancing progress — comparing the default path of progress to one that is shifted earlier. There might be other claims about the value of progress that are unaffected. For example, these considerations don’t directly undermine the argument that progress is better than stasis, and thus that if progress is fragile, we need to protect it. That may be true even if humanity does eventually bring about its own end, and even if our progress brings it about sooner. Or one could understand ‘progress’ to refer only to those cases where the outcomes are genuinely improved, such that it is by definition a good thing. But the arguments we’ve explored show that these other arguments in favour of progress wouldn’t have many of the policy implications that advocates of progress typically favour — as whether it is good or bad to advance scientific research or economic productivity will still depend very sensitively on esoteric questions about how humanity ends.

⁂ 

I find all this troubling. I’m a natural optimist and an advocate for progress. I don’t want to see the case for advancing progress undermined. But when I tried to model it clearly to better understand its value, I found a substantial gap in the argument. I want to draw people’s attention to that gap in the hope that we can close it. There may be good arguments to settle this issue one way or the other, but they will need to be made. Alternatively, if we do find that uniform advancements of progress are in fact bad, we will need to adjust our advocacy to champion the right kinds of differential progress.

---

$^1$ I’d like to thank Fin Moorhouse, Kevin Kuruc, and Chad Jones for insightful discussion and comments, though of course this doesn’t imply that they endorse the arguments in this paper.

$^2$ The arguments in this paper would also apply if it were instead a temporary acceleration leading to a permanent speed-up of progress. In that case an endogenous end time would mean a temporal compression of our trajectory up to that point: achieving all the same quality levels, but having less time to enjoy each one, then prematurely ending.

$^3$ This is proved in more detail, addressing several complications in Ord (forthcoming). Several complexities arise from different approaches to population ethics, but the basic argument holds for any approach to population ethics that considers a future with lower total and average wellbeing to be worse. If your approach to population ethics avoids this argument, then note that whether advancing progress is good or bad is now highly sensitive to the theory of population ethics — another contentious and esoteric topic.

$^4$ One could generalise this argument beyond human extinction. First, one could consider other kinds of existential risk. For instance, if a global totalitarian regime arises which permanently reduces quality of life to a lower level than it is today, then what matters is whether the date of its onset is endogenous. Alternatively, we could broaden this argument to include decision-makers who are partial to a particular country or culture. In that case, what matters is whether advancing progress would advance the end of that group.

$^5$ For example, if final years are 10 times as good as present years, then we would only need a 10% chance that humanity’s end was exogenous for advancing progress to be good in expectation. I think this is a promising strategy for saving the expected value of progress.

$^6$ In this setting, the former idea of an endogenous end time roughly corresponds to the assumption that advancing progress by a year also shifts humanity’s survival curve left by a year, while an exogenous end time corresponds to the assumption that the survival curve stays fixed. A third salient possibility is that it is the corresponding hazard curve which shifts left by a year. This possibility is mentioned in Ord (forthcoming, pp. 17 & 30). The first and third of these correspond to what Bostrom (2014) calls transition risk and state risk.

$^7$ For example, one could decompose the overall hazard curve into an exogenous hazard curve plus an endogenous one, where only the latter gets shifted to the left. Alternatively, Aschenbrenner & Trammell (2024) present a promising parameterisation that interpolates between state risk and transition risk (and beyond).

$^8$ See, for example, my book on existential risk (Ord 2020), or the final section of Ord (forthcoming).

$^9$ See Moynihan (2020).

$^{10}$ Any substantial change to the future, including advancing progress by a year, would probably have large chaotic effects on the future in the manner of the butterfly effect. But only a systematic change to the expected shape or duration of the curve, could help save the initial case for advancing progress.

$^{11}$ The fossil record suggests natural extinction risk is lower than 1 in 1,000 per century — after all humanity has already survived 2,000 centuries and typical mammalian species survive 10,000 centuries. See Snyder-Beattie et al. (2019) and Ord (2020, pp. 80–87).

$^{12}$ Another kind of case that is often made is that the sheer rate of progress could change the future trajectory. A common version is that the world is more stable with steady 3–5% economic growth: if we don’t keep moving forward, we will fall over. This is plausible but gives quite a different kind of conclusion. It suggests it is good to advance economic progress when growth is at 2% but may be bad to advance it when growth is 5%. Moreover, unless the central point about progress bringing forward humanity’s end is dealt with head-on, the best this steady-growth argument can achieve is to say that ‘yes, advancing progress may cut short our future, but unfortunately we need to do it anyway to avoid collapse’.

$^{13}$ Beckstead calls this kind of change to where we’re going, rather than just how quickly we get there a ‘trajectory change’ (Beckstead 2013).

$^{14}$ Bostrom’s concept of differential technological development (Bostrom 2002) is a special case.

References

Aschenbrenner, Leopold; and Trammell, Philip. (2024). Existential Risk and Growth. GPI Working Paper No. 13-2024, (Global Priorities Institute and Department of Economics, University of Oxford).

Beckstead, Nick. (2013). On the Overwhelming Importance of Shaping the Far Future. PhD Thesis. Department of Philosophy, Rutgers University.

Bostrom, Nick. (2002). Existential Risks: Analyzing Human Extinction, Journal of Evolution and Technology 9(1).

Bostrom, Nick. (2014). Superintelligence: Paths, dangers, strategies, (Oxford: OUP).

Moynihan, Thomas. (2020). X-Risk: How Humanity Discovered its Own Extinction, (Urbanomic).

Ord, Toby. (2020). The Precipice: Existential risk and the Future of Humanity, (London: Bloomsbury).

Ord, Toby. (Forthcoming). Shaping humanity’s longterm trajectory. In Barrett et al (eds.) Essays on Longtermism, (Oxford: OUP).

Snyder-Beattie, Andrew E.; Ord, Toby; and Bonsall, Michael B. (2019). An upper bound for the background rate of human extinction. Scientific Reports 9:11054, 1–9.

29 June 2024

Robust Longterm Comparisons

The choice of discount rate is crucially important when comparing options that could affect our entire future. Except when it isn’t. Can we tease out a class of comparisons that everyone can agree on regardless of their views on discounting?

Some of the actions we can take today may have longterm effects — permanent changes to humanity’s longterm trajectory. For example, we may take risks that could lead to human extinction. Or we might irreversibly destroy parts of our environment, creating permanent reductions in the quality of life.

Evaluating and comparing such effects is usually extremely sensitive to what economists call the pure rate of time preference, denoted ρ. This is a way of encapsulating how much less we should value a benefit simply because it occurs at a later time. There are other components of the overall discount rate that adjust for the fact that an extra dollar is worth less when people are richer, that later benefits may be less likely to occur — or that the entire society may have ceased to exist by then. But the pure rate of time preference is the amount by which we should discount future benefits even after all those things have been accounted for.

Most attempts to evaluate or compare options with longterm effects get caught up in intractable disagreements about ρ. Philosophers almost uniformly think ρ should be set to zero, with any bias towards the present being seen as unfair. That is my usual approach, and I’ve developed a framework for making longterm comparisons without any pure time preference. While some prominent economists agree that ρ should be zero, the default in economic analysis is to use a higher rate, such as 1% per year.

The difference between a rate of 0% and 1% is small for most things economists evaluate, where the time horizon is a generation or less. But it makes a world of difference to the value of longterm effects. For example, ρ = 1% implies that a stream of damages starting in 500 years time and lasting a billion years is less bad than a single year of such damages today. So when you see a big disagreement on how to make a tradeoff between, say, economic benefits and existential risk, you can almost always pinpoint the source to a disagreement about ρ.

This is why it was so surprising to read Charles Jones’s recent paper: ‘The AI Dilemma: Growth versus Existential Risk’. In his examination of whether and when the economic gains from developing advanced AI could outweigh the resulting existential risk, the rate of pure time preference just cancels out. The value of ρ plays no role in his primary model. There were many other results in the paper, but it was this detail that grabbed my attention.

Here was a question about trading off risk of human extinction against improved economic consumption that economists and philosophers might actually be able to agree on. After all, even better than picking the correct level of ρ, deriving the correct conclusion, and yet still having half the readers ignore your findings, is if there is a way of conducting the analysis such that you are not only correct — but that everyone else can see that too.

Might we be able to generalise this happy result further?

• Is there are broader range of long run effects in which the discount rate still cancels out?

• Are there other disputed parameters (empirical or normative) that also cancel out in those cases?

What I found is that this can indeed be greatly generalised, creating a domain in which we can robustly compare long run effects — where the comparisons are completely unaffected by different assumptions about discounting.

⁂

Let’s start by considering a basic model where $u(t)$ represents the ‘instantaneous utility’ or ‘flow utility’ of a representative person at time $t$. That is, it is a measure of their wellbeing such that the integral of $u(t)$ over a period of time is the utility (or wellbeing) the person accrued over that period. This is normalised such that the zero level for $u(t)$ is the level where someone is indifferent about adding a period at this level to their life.

Now let $n(t)$ represent the number of people alive at time $t$ and let $d(t)$ be the discount factor for time $t$. This discount factor is another way of expressing pure time preference. A constant rate of pure time preference ρ, corresponds to a discount factor that drops exponentially over time: $d(t) = e^{–ρt}$. But $d(t)$ need not drop exponentially — indeed it could be any function at all. So could $n(t)$ and $u(t)$. The only constraints are that they are all integrable functions and that the integral below converges to a finite value.

On this model, we’ll say the value of the entire longterm future is:

$V = \int_0^\infty d(t) \cdot n(t) \cdot u(t) \ . \ dt$

(This equation assumes the total view in population ethics, where we add up everyone’s utility, but we’ll see later that this can be relaxed.)

Now suppose that we have the possibility of improving the quality of life, from $u(t)$ to some other curve $u^+(t)$, without altering $d(t)$ or $n(t)$. And lets make a single substantive assumption: that this improvement is a rescaling of the original pattern of flow utility: $u^+(t) = k \ u(t)$ for some scaling factor $k$. How does this change the value of the future?

$V^+ = \int_0^\infty d(t) \cdot n(t) \cdot k \ u(t) \ . \ dt$

$V^+ = k \int_0^\infty d(t) \cdot n(t) \cdot u(t) \ . \ dt$

$V^+ = k V$

So on this model, scaling up a curve of utility over time simply leads to scaling up the discounted total value under that curve.

What about the value of extinction? We can model extinction here by $n(t)$ going to zero. If so, the value of the integral from that point on falls to zero. (Similarly, other kinds of existential catastrophe could be modelled as $u(t)$ going to zero.)

Now let’s consider the expected value of developing a risky technology, where we have a probability $s$ of surviving the development process and scaling up all future utility by a factor of $k$, but otherwise we go extinct.

$EV$(develop)$\ = s V^+ + (1-s)0 = s V^+ = s k V$

This expected value still depends on the the discount function $d(t)$ because $V$ depends on $d(t)$. But what if we ask about the decision boundary between when the expected value of taking the risk ($EV$(develop)) is better or worse than the value of the status quo ($V$). The boundary occurs when they are equal:

$EV$(develop)$\ = V$

So:

$skV = V$

$s = \frac{1}{k}$

This decision boundary for comparing whether it is worth taking on a risk of extinction to make a lasting improvement to our quality of life has no dependence on the discount function $d(t)$. Nor does it depend on the population curve $n(t)$. And because it doesn’t depend on the population curve, the decision doesn’t depend on whether we weight time periods by their populations or not. It is thus at the same place for either of the two most commonly used version of population ethics within economics: the time integral of total flow utility and the time integral of average flow utility.

And one can generalise even further.

This model assumed that all the extinction risk (if any) happens immediately. But we might instead want to allow for any pattern of risk occuring over time. We can do this via a survival curve, where the chance of surviving at least until $t$ is denoted $S(t)$. This can be any (integrable) non-increasing function that starts at 1. If so, then the expected value of the status quo goes from:

$V = \int_0^\infty d(t) \cdot n(t) \cdot u(t) \ . \ dt$

to

$EV = \int_0^\infty S(t) \cdot d(t) \cdot n(t) \cdot u(t) \ . \ dt$

And this has simply placed another multiplicative factor inside the integral. So as long as the choice we are considering doesn’t alter the pattern of existential risk in the future, the argument above still goes through. Thus the decision boundary is independent of the future pattern of extinction risk (if that is unchanged by the decision in question).

Jones’s model has more economic detail than this, but ultimately it is a special case of the above. He considers only constant discount rates (= exponential discount functions), assumes no further risk beyond the initial moment, and that the representative flow utility of the status quo, $u(t)$, is constant. He considers the possibility of it changing to some other higher constant level $u^+(t)$, which can be considered a scaled up version of $u(t)$, where $k = \frac{u^+(0)}{u(0)}$.

So the argument above generalises Jones’s class of cases where comparisons of longterm effects are independent of discounting in the following ways:

• constant $u(t)$ and $u^+(t)$  $\Rightarrow$  $u(t)$ may vary and $u^+(t)=k\ u(t)$

• constant ρ  $\Rightarrow$  time-varying ρ (so long as value converges)

• constant population growth rate $\Rightarrow$ exogenous time-varying population growth

• total view of population ethics  $\Rightarrow$  either total or time integral of average

• no further extinction risk $\Rightarrow$ exogenous time-varying extinction risk

It is worthing noting that Jones’s model is addressing the longterm balance of costs and benefits of advance AI via a question like this:

if we could either get the benefits of advanced AI at some risk to humanity, or never develop it at all, which would be best?

This is an important question, and one where (interestingly) the way we discount may not matter. On his model it roughly boils down to this: it would be worth reducing humanity’s survival probability from 100% down to $s$ whenever we can thereby scale up the representative utility by a factor of $1/s$.

In some ways, this is obvious — being willing to risk a 50% chance of death to get some higher quality of life is arguably just what it means for that new quality level to be twice the old one. But its implications may nonetheless surprise. After all, it is quite believable that some technologies could make life 10 times better, but a little disconcerting that it would be worth a 90% chance of human extinction to reach them.

One observation that makes this implication a little less surprising is to note that there may be ways to reach such transformative technologies for a lesser price. Just because it may be worth a million dollars to you to get a bottle of water when dying of thirst, doesn’t mean it is a good deal when there is also a shop selling bottles of water for a dollar apiece. Those people who are leading the concern about existential risk from AI are not typically arguing that we should forgo developing it altogether, but that there is a lot to be gained by developing it more slowly and carefully. If this reduces the risk even a little, it could be worth quite a lengthy delay to the stream of benefits. Of course this question of how to trade years of delay with probability of existential risk does depend on how you discount. Alas.

⁂

In my own framework on longterm trajectories of humanity, I call anything that linearly scales up the entire curve of instantaneous value over time an enhancement. And I showed that like the value of reducing extinction risk, the value of an enhancement scales in direct proportion to the entire value of the future, which makes comparisons between risk reduction and enhancements particularly easy (much as we’ve seen here). But in that framework, there was an explicit assumption of no pure time preference, so I had no cause to notice how ρ (or equivalently, $d(t)$) completely cancels out of the equations. So this a nice addition to the theory of how to compare enhancements to risk reduction.

One might gloss the key result about robustness to discounting procedure as follows:

When weighing the benefits of permanently scaling up quality of life against a risk of extinction, the choice of discounting procedure makes no difference — nor does the population growth rate or subsequent pattern of extinction risk (so long as these remain the same).

In cases like these, discounting scales down the magnitude of the future benefits and of the costs in precisely the same way, but leaves the location where benefits equal the costs alone. It can thus make a vast difference to evaluations of future trajectories, but no difference at all to comparisons.

I hope that this region of robustness to the choice of discounting might serve as an island of agreement between people studying these questions, even when they come from very different traditions regarding valuing the future. Moreover, the fact that the comparison is robust to the very uncertain questions of the population size and survival curve for humanity across aeons to come, shows that at least in some cases we can still compare longterm futures despite our deep uncertainty about how the future may unfold.

15 May 2024

The timing of labour aimed at reducing existential risk

Work towards reducing existential risk is likely to happen over a timescale of decades. For many parts of this work, the benefits of that labour are greatly affected by when it happens. This has a large effect when it comes to strategic thinking about what to do now in order to best help the overall existential risk reduction effort. I look at the effects of nearsightedness, course setting, self-improvement, growth, and serial depth, showing that there are competing considerations which make some parts of labour particularly valuable earlier, while others are more valuable later on. We can thus improve our overall efforts by encouraging more meta-level work on course setting, self-improvement, and growth over the next decade, with more of a focus on the object-level research on specific risks to come in decades beyond that.

Nearsightedness

Suppose someone considers AI to be the largest source of existential risk, and so spends a decade working on approaches to make self-improving AI safer. It might later become clear that AI was not the most critical area to worry about, or that this part of AI was not the most critical part, or that this work was going to get done anyway by mainstream AI research, or that working on policy to regulate research on AI was more important than working on AI. In any of these cases she wasted some of the value of her work by doing it now. She couldn’t be faulted for lack of omniscience, but she could be faulted for making herself unnecessarily at the mercy of bad luck. She could have achieved more by doing her work later, when she had a better idea of what was the most important thing to do.

We are nearsighted with respect to time. The further away in time something is, the harder it is to perceive its shape: its form, its likelihood, the best ways to get purchase on it. This means that work done now on avoiding threats in the far future can be considerably less valuable than the same amount of work done later on. The extra information we have when the threat is up close lets us more accurately tailor our efforts to overcome it.

Other things being equal, this suggests that a given unit of labour directed at reducing existential risk is worth more the later in time it comes.

Course setting, self-improvement & growth

As it happens, other things are not equal. There are at least three major effects which can make earlier labour matter more.

The first of these is if it helps to change course. If we are moving steadily in the wrong direction, we would do well to change our course, and this has a larger benefit the earlier we do so. For example, perhaps effective altruists are building up large resources in terms of specialist labour directed at combatting a particular existential risk, when they should be focusing on more general purpose labour. Switching to the superior course sooner matters more, so efforts to determine the better course and to switch onto it matter more the earlier they happen.

The second is if labour can be used for self-improvement. For example, if you are going to work to get a university degree, it makes sense to do this earlier in your career rather than later as there is more time to be using the additional skills. Education and training, both formal and informal, are major examples of self-improvement. Better time management is another, and so is gaining political or other influence. However this category only includes things that create a lasting improvement to your capacities and that require only a small upkeep. We can also think of self-improvement for an organisation. If there is benefit to be had from improved organisational efficiency, it is generally better to get this sooner. A particularly important form is lowering the risk of the organisation or movement collapsing, or cutting off its potential to grow.

The third is if the labour can be used to increase the amount of labour we have later. There are many ways this could happen, several of which give exponential growth. A simple example is investment. An early hour of labour could be used to gain funds which are then invested. If they are invested in a bank or the stock market, one could expect a few percent real return, letting you buy twice as much labour two or three decades later. If they are invested in raising funds through other means (such as a fundraising campaign) then you might be able to achieve a faster rate of growth, though probably only over a limited number of years until you are using a significant fraction of the easy opportunities.

A very important example of growth is movement building: encouraging other people to dedicate part of their own labour or resources to the common cause, part of which will involve more movement building. This will typically have an exponential improvement with the potential for double digit percentage growth until the most easily reached or naturally interested people have become part of the movement at which point it will start to plateau. An extra hour of labour spent on movement building early on, could very well produce a hundred extra hours of labour to be spent later. Note that there might be strong reasons not to build a movement as quickly as possible: rapid growth could involve increasing the signal to noise ratio in the movement, or changing its core values, or making it more likely to collapse, and this would have to be balanced against the benefits of growth sooner.

If the growth is exponential for a while but will spend a lot of time stuck at a plateau, it might be better in the long term to think of it like self improvement. An organisation might have been able to raise \$10,000 of funds per year (after costs) before the improvement and then gains the power to raise \$1,000,000 of funds per year afterwards — only before it hits the plateau does it have the exponential structure characteristic of growth.

Finally, there is a matter of serial depth. Some things require a long succession of stages each of which must be complete before the next begins. If you are building a skyscraper, you will need to build the structure for one story before you can build the structure for the next. You will therefore want to allow enough time for each of these stages to be completed and might need to have some people start building soon. Similarly, if a lot of novel and deep research needs to be done to avoid a risk, this might involve such a long pipeline that it could be worth starting it sooner to avoid the diminishing marginal returns that might come from labour applied in parallel. This effect is fairly common in computation and labour dynamics (see The Mythical Man Month), but it is the factor that I am least certain of here. We obviously shouldn’t hoard research labour (or other resources) until the last possible year, and so there is a reason based on serial depth to do some of that research earlier. But it isn’t clear how many years ahead of time it needs to start getting allocated (examples from the business literature seem to have a time scale of a couple of years at most) or how this compares to the downsides of accidentally working on the wrong problem.

Consequences

We have seen that nearsightedness can provide a reason to delay labour, while course setting, self-improvement, growth, and serial depth provide reasons to use labour sooner. In different cases, the relative weights of these reasons will change. The creation of general purpose resources (such as political influence, advocates for the cause, money, or earning potential) is especially resistant to the nearsightedness problem as they have more flexibility to be applied to whatever the most important final steps happen to be. Creating general purpose resources, or doing course setting, self-improvement, or growth are thus comparatively better to do in the earlier times. Direct work on the cause is comparatively better to do later on (with a caveat about allowing enough time to allow for the required serial depth).

In the case of existential risk, I think that many of the percentage points of total existential risk lie decades or more in the future. There is quite plausibly more existential risk in the 22nd century than in the 21st. For AI risk, the recent FHI survey of 174 experts, the median estimate for when there would be a 50% chance of reaching roughly human level AI was 2040. For the subgroup of those who are part of the ‘Top 100’ researchers in AI, it was 2050. This gives something like 25 to 35 years before we think most of this risk will occur. That is a long time and will produce a large nearsightedness problem for conducting specific research now and a large potential benefit for course setting, self-improvement, and growth. Given a portfolio of labour to reduce risk over that time, it is particularly important to think about moving types of labour towards the times where they have a comparative advantage. If we are trying to convince others to help use their careers to reduce this risk, the best career advice might change over the coming decades from help with movement building or course setting, to accumulating more flexible resources, to doing specialist technical work.

The temporal location of a unit of labour can change its value by a great deal. It is quite plausible that due to nearsightedness, doing specific research now could have less than a tenth the expected value of doing it later, since it could so easily be on the wrong risk, or the wrong way of addressing the risk, or would have been done anyway, or could have been done more easily using tools people later build etc. It is also quite plausible that using labour to produce growth now, or to point us in a better direction, could produce ten times as much value. It is thus pivotal to think carefully about when we want to have different kinds of labour.

I think that this overall picture is right and important. However, I should add some caveats. We might need to do some specialist research early on in order to gain information about whether the risk is credible or which parts to focus on, to better help us with course setting. Or we might need to do research early in order to give research on risk reduction enough academic credibility to attract a wealth of mainstream academic attention, thereby achieving vast growth in terms of the labour that will be spent on the research in the future. Some early object level research will also help with early fundraising and movement building — if things remain too abstract for a long time, it would be extremely difficult to maintain a movement. But in these examples, the overall picture is the same. If we want to do early object-level research, it is because of its instrumental effects on course setting, self-improvement, and growth.

The writing of this document and the thought that preceded it are an example of course setting: trying to significantly improve the value of the long-term effort in existential risk reduction by changing the direction we head in. I think there are considerable gains here and as with other course setting work, it is typically good to do it sooner. I’ve tried to outline the major systematic effects that make the value of our labour vary greatly with time, and to present them qualitatively. But perhaps there is a major effect I’ve missed, or perhaps some big gains by using quantitative models. I think that more research on this would be very valuable.

3 July 2014

A Child's Plaything

Imagine if we could somehow show the people of the eighteenth century a simple child’s toy from today — say, a speaking doll.

The common folk would marvel at its ability to speak its few stock phrases. The scientists and engineers would marvel even more at its innards; at the minutely detailed silicon; at the bewildering complexity soon to be within their grasp.

But the economists would be amazed. For this design — so far beyond the peak of their world’s powers — was not a gift for a King or Queen, but clearly just a child’s toy. And not just that. The very banality of the toy, the artlessness of the sculpting and the way the paint doesn’t even quite line up with the contours of the doll’s face, prove that this is not the toy of a prince — but of poor child. And they would understand that the people of our time are so wealthy, so powerful, that every one of them has access to machines with thousands of parts working in concert, and that it is less effort to build such a wondrous machine than to simply paint a doll’s eyebrows in their right places.

27 March 2023

Remembering Peter Eckersley

A eulogy for Peter Eckersley
Delivered at his official memorial service
Internet Archive, San Francisco, 4 March 2023

Twenty-six years ago, I sat down in an underground room at Melbourne University. A hall of identical computers. Next to me was a stylish young man with this on his screen:

View fullsize

I couldn’t believe it. My screen was all grey, with a single blue window with white text.

“How did you get it to look like that?” I asked.

“Well, you just need to ‘gvim .fvwm2rc’,” he replied.

“What?”

“No problem, I’ll just send you all my config files and set you up…”

And that was the beginning of a long friendship…

I still love his colour choices. So enduringly Peter. The decadence of the purple and gold, on a green silk waistcoat-ish background. I eventually changed my own background to Waterhouse's Lady of Shallot and sampled colours from her candles and silks for my text and accents. When we got our own websites, they each inherited our unix colour schemes, and our digital identities forked off from that meeting into our own directions, with traces still visible and ongoing…

I was in my first year, and Peter his second. Over our undergraduate years, our friendship grew.

Here is my first ever photo of Peter (on the right) in 1998:

View fullsize

After a protest march, we had pitched tents in the middle of the most sacred quad at Melbourne University and were in a student politics meeting under the camellia trees at midnight.

View fullsize

Here’s a more typical shot in 2000, at my 21st.

We shared a deep thirst for ideas and a taste for wonder. We would talk about science and technology, about ethics and the nature of reality late, late into the night.

Indeed, while he was chiefly a technologist, he is among the people who have thought the deepest about the long term fate of a universe shaped by intelligence and directed by moral values — about the limits of what we could achieve over the aeons ahead. And he was a natural philosopher too, with original contributions on the paradoxes at the heart of population ethics. Over the years, we talked about the big picture questions facing humanity, about global poverty and existential risk, and the ideas that would become effective altruism. When I started Giving What We Can in 2009, he was one of 23 founding members, making a lifelong pledge to donate a tenth of his income to the most cost-effective charities he could find. He wrote:

"For me, taking a pledge to give is exciting.  I've long been persuaded that it would be better to use a good portion of my income to support very effective aid projects, but it's hard to know what they are, and often easier to spend money on luxuries that in the end aren't particularly necessary for happiness.  A pledge is a way to ensure that I do what I already wanted to, a way to meet a community of people who think the same way, and a way to work together on finding the most effective projects to contribute to."

Indeed he continues to guide my vision of effective altruism. Last week I ended my keynote talk with a slide about the importance of good character for all of us dedicated to helping others as much as we can. The picture I painted of integrity and earnestness was a picture of Peter.

We also shared an enduring love of beauty. I never found out exactly the form his ideal future might take. But it would be a place of freedom, and wonder, and friends. And beauty everywhere.

In 2003 I left Melbourne to go to the dreaming spires of Oxford and study philosophy. He stayed in Melbourne, transferring from a PhD in Computer Science to one in Law — trying to understand how to refashion an economic system based on physical goods to one fit for virtual goods — songs and stories and ideas that once created can be copied freely. A few years later, he got his dream job offer, from the Electronic Frontiers Foundation, in faraway San Francisco.

Little did he know, but it would become his home. He would find a subculture within it that was like a distillation of the one he moved in in Melbourne. Let me share his first thoughts on San Francisco:

Hi guys,

I've been in San Francisco a week, and it's definitely time for an email of stories.

I'm sitting on a "sidewalk" as I write this, on a little timber bench with a coffee and a gorgeous bamboo plant next to me (photo attached :). There's a corset shop next door.  As soon as I opened my laptop, I got roped into a conversation with a bunch of geeks -- one of them was asking for advice about Internet regulation in Japan; another worked for Google and was asking me to let them keep their files on everybody.  This city is completely packed with nerds; random conversations with them seem to be a regular occurrence.

Working at EFF is remarkable.  The organisation is a nerve center for more lawsuits than you could sensibly imagine.  Many -- but not all -- of these are a little depressing.  Except when they sue purple dinosaurs.  My first week has been very busy, but I don't yet have a sense of how normal this is.  Aside from numerous administrative diversions, I've been busy writing a white paper on how to keep your web search history private (a surprisingly hard thing to do).  The other three technical staff will be away next week -- go and google Burning Man -- so I'm going to find out if I can administer and support the EFF's computer infrastructure too.

The bike culture here is definitely stronger than in Melbourne. Especially where I work, there are bikes everywhere.  There also seems to be way more bike Bling.  There's this strange subcultural species of people known as "hipsters".  Bicycle fashion is an important part of this.  Often, they're on fixies, but not always.  See, for example, the attached photo of a vague-seeming girl cruising around on a $5,000 bicycle made of bamboo and carbon fibre.

…

I haven't found a house yet.  It's back-to-school season, and judging from what I saw at an open house this afternoon, I might not find one for a few weeks.  Fortunately, I can continue to sleep in Seth's incredibly precarious spare loft.  Getting out of bed in the morning involves hopping onto an a free-standing step ladder.  It wakes you up!

Anyway, I'm going to go and explore the corsetry.  I'm missing you all. I'll try and set up a website somewhere so that I'm not filling your inboxes with my excessive verbosity (speaking of which, I haven't actually attached any photos but you can see them at http://www.cs.mu.oz.au/~pde/pics/sf/ ).

Let me know what's happening in Melbourne...

P.

Sadly his ‘attached’ pictures are lost to bit rot, but I was looking through all my old photos, and found this — a photo of Peter I took five years later which (given the bamboo and corset shop) must be the exact spot he was sitting when he wrote his email.

View fullsize

We kept up over the decades, with trips back and forth between our new cities. Here he is in 2008:

View fullsize

And here are the two of us after we cycled up to Coit tower:

View fullsize

Here he is in 2011, looking out over his adopted home:

View fullsize

It was only after his death that I got a glimmer of just how much he did for the internet over his sixteen years in San Francisco — especially privacy and security. It was only then that I really reflected on how wildly important the internet is, yet how there is no-one whose responsibility it is to keep it going, and to improve it. It is like we are at sea on a great old sailing ship. But there is no captain, and no owner. Peter, is one of a few people who didn’t stand idly by, but stood up and took on the responsibility. We couldn’t even take the ship in to dock, so Peter and others at the EFF took on the crazy, yet essential, task of repairing and rebuilding it at sea…

Peter loved forming connections with people. It was only in the outpouring of emotion after his death that I realised how great a part of his life that was. It was a flood of love for him so strong that for a shining moment even Twitter was a place of beauty and wonder.

And I saw how he had made such strong connections with so many people. A node in a network with thousands of strands radiating out from him. I think he measured his wealth in friends, and was a friend-millionaire. But that wasn’t enough. He was too good a computer scientist to be happy with a network like that. It was too brittle, too vulnerable. So he set about making connections between all those other nodes — connecting people who didn’t know they needed each other.

We’re now a network with a missing node at its centre. But we haven’t fallen apart. Because of what he started, there are hundreds of cross-linking paths between us. And we’re not done. Even with a missing node, one can bridge the gap. I’ve only been back here a week, and there are so many conversations with strangers, where my spidey senses tingled and I’ve stopped and asked “Did you know Peter?” — and often they did. And just like that, a connection formed.

So this grand overarching project of Peter’s life is not done. But now it’s up to us to make our own introductions to each other, to fill out this grand network, to find those he would have found for us.

And what better way could there be to honour him?

4 March 2023

Casting the Decisive Vote

What is the chance your vote changes the outcome of an election? We know it is low, but how low?

In particular, how does it compare with an intuitive baseline of a 1 in $n$ chance, where $n$ is the number of voters? This baseline is an important landmark not only because it is so intuitive, but because it is roughly the threshold needed for voting to be justified in terms of the good it produces for the members of the community (since the total benefit is also going to be proportional to $n$).

Some political scientists have tried to estimate it with simplified theoretical models involving random voting. Depending on their assumptions, this has suggested it is much higher than the baseline — roughly 1 in $\sqrt{n}$ (Banzhaf 1965) — or that it is extraordinarily lower — something like 1 in $10^{2,659}$ for a US presidential election (Brennan 2011).

Statisticians have attempted to determine the chance of a vote being decisive for particular elections using detailed empirical modelling, with data from previous elections and contemporaneous polls. For example, Gelman et al (2010) use such a model to estimate that an average voter had a 1 in 60 million chance of changing the result of the 2008 US presidential election, which is about 3 times higher than the baseline.

In contrast, I’ll give a simple method that depends on almost no assumptions or data, and provides a floor for how low this probability can be. It will calculate this using just two inputs: the number of voters, $n$, and the probability of the underdog winning, $p_u$.

The method works for any two-candidate election that uses simple majority. So it wouldn’t work for the US presidential election, but would work for your chance of being decisive within your state, and could be combined with estimates that state is decisive nationally. It also applies for many minor ‘elections’ you may encounter, such as the chance of your vote being decisive on a committee.

We start by considering a probability distribution over what share of the vote a candidate will get, from 0% to 100%. In theory, this distribution could have any shape, but in practice it will almost always have a single peak (which could be at one end, or somewhere in between). We will assume that the probability distribution over vote share has this shape (that it is ‘unimodal’) and this is the only substantive assumption we’ll make.

We will treat this as the probability distribution of the votes a candidate gets before factoring in your own vote. If there is an even number of votes (before yours) then your vote matters only if the vote shares are tied. In that case, which way you vote decides the election. If there is an odd number of votes (before yours), it is a little more complex, but works out about the same: Before your vote, one candidate has one fewer vote. Your vote decides whether they lose or tie, so is worth half an election. But because there are two different ways the candidates could be one vote apart (candidate A has one fewer or candidate B has one fewer), you are about twice as likely to end up in this situation, so have the same expected impact. For ease of presentation I’ll assume there is an even number of voters other than you, but nothing turns on this.

(In real elections, you may also have to worry about probabilistic recounts, but if you do the analysis, these don’t substantively change anything as there is now a large range of vote shares within which your vote improves the probability that your candidate secures a recount, wins a recount, or avoids a recount (Gelman et al 2002, p 674).)

So we are considering a unimodal probability distribution over the share of the vote a candidate will get and we are asking what is the chance that the share is exactly 50% (with an even number of voters). This corresponds to asking what is the height of the distribution in the very centre. Our parameters will be:

$n$ — the number of voters (other than you).

$p_u$ — the probability that the underdog would win (without you voting). 

$p_d$ — the probability that your vote is decisive.

Our job is to characterise $p_d$ in terms of the inputs $n$ and $p_u$. It is impossible to determine it precisely, but it is surprisingly easy to produce a useful lower bound.

The key observation is that as the distribution has a single mode, there must be at least one side of the distribution that doesn’t have the mode on it. That side is monotonically increasing (or at least non-decreasing) as one proceeds from the outside towards the centre. How low could the centre be? Well the entire non-decreasing side either has probability $p_u$ or $1-p_u$, so the minimum probability it could have is $p_u$. And the way of spreading it out that would lead to the lowest value in the centre is if it were uniformly distributed over that side (over the $\frac{n}{2}$ outcomes ranging from the candidate getting all the vote through to getting just over half).

In this case, the probability in the exact centre (i.e. the probability of a decisive vote) must be at least $p_u \div \frac{n}{2}$. In other words:

$$p_d \geq \frac{2p_u}{n}$$

This is highest when the candidates have equal chances ($p_u \approx$ 50%). Then the lower bound for having a decisive vote is simply $\frac{1}{n}$ — the intuitive baseline. The bound decreases linearly as the underdog’s chances decrease. So for example, if the underdog has a 10% chance, the bound for a decisive vote is $\frac{1}{5n}$, and if they have a 1% chance, it is $\frac{1}{50n}$.

So for simple elections that are not completely forgone conclusions, the chance of having a decisive vote can’t be all that much lower than $\frac{1}{n}$. 

What does probability mean here?

This analysis works for several kinds of probability, so long as the probability of the underdog winning and the probability of your vote being decisive are of the same type. So if you have a 10% degree of belief that the underdog will win, you are rationally required to have at least a $\frac{1}{5n}$ degree of belief that your vote will be decisive. And if the best informed and calibrated political models assign a 10% chance to the underdog winning, then they also need to assign at least a $\frac{1}{5n}$ chance to your vote being decisive.

What if a larger majority is required?

The earlier analysis generalises very easily. Now instead of estimating the height of the distribution at the centre, we do so it at the supermajority point (e.g. $\frac{2}{3}$). The worst case is when the non-decreasing side is also the longer side, so the probability gets spread thinner across these possibilities, giving:

$$p_d \geq \frac{p_u}{nm}$$

where $m$ is the size of the majority needed (i.e. a simple majority has $m = \frac{1}{2}$, a two-thirds majority has $m = \frac{2}{3}$). 

Can we relax the assumption that the distribution is unimodal?

Our only use of this assumption was to prove that there was a side of the distribution with no mode on it. So we could replace the assumption with that weaker claim.

It wouldn’t matter if there were multiple modes, so long as they are all on the same side of the distribution. The problem with multiple modes is that there could be one on either side, with almost all the probability mass gathered near them, and a negligible amount in between at the centre. But this seems very implausible as a credence distribution in advance of an election. And even if somehow your beliefs were that it was probably going to be a landslide one way or the other, you can sometimes still apply this bound:

e.g. Suppose your credences were a mixture of (1) a very skewed unimodal distribution with 95% chance of candidate A winning and (2) another such distribution with 95% chance of candidate B winning. That would still just be the same chance of being decisive as in an election where the underdog has a 5% chance of winning (after all, you can see this as being certain the underdog has a 5% chance, you just don’t know which candidate is the underdog), and that would still leave you with a $\frac{1}{10n}$ chance of having the decisive vote.

Multi-level elections?

Many elections proceed in two stages, with individual voters electing representatives for their constituency or state, and then those representatives having their own election (e.g. for the right to appoint the president or prime minister). If each constituency has equal voting power in the higher level election, then one can simply apply my model twice. 

e.g. if there are $n_1$ people in your constituency and a 25% chance of the local underdog winning it, then you have at least a $\frac{1}{2n_1}$ chance of determining your constituency’s representative. If there are $n_2$ constituencies in the nation with a 10% chance of the national underdog winning a majority of them (conditional upon your own constituency being tied), then there is at least a $\frac{1}{5n_2}$ chance of your constituency being nationally decisive. The chance your vote is nationally decisive is then the product of these: $\frac{1}{10n_1n_2}$.

In general, the formula is just:

$$p_d \geq \frac{2 p_{u1}}{n_1} × \frac{2p_{u2}}{n_2}  =  \frac{4p_{u1}p_{u2}}{n_1n_2}$$

If the constituencies are roughly equally sized, then $n_1 n_2 \approx n$, so for a competitive election and a competitive electorate, the chance of being decisive is still not much worse than the baseline of $\frac{1}{n}$.

Note that because this involves applying a conservative lower bound twice in succession, it will tend to give probabilities that are a bit lower than if it were a simple one-level election. This may just be due to the conservativeness of focusing on worst case scenarios rather than suggesting that the two level structure actually lowers the chance of having a decisive vote.

If constituencies have different voting power (as in the US electoral college) or if some have incumbents whose seats aren’t up for re-election (as in the US senate) there are additional complications and you may want to turn to a specific model crafted for that election.

Comparisons with other work

The most prominent theoretical model for the probability of a decisive vote is the random voting model. It assumes that all other voters vote randomly, voting for candidate A with a probability $p_A$, which must be exactly the same for all voters. This is the background for Banzhaf’s (1965) result that $p_D \approx$ 1 in $\sqrt{n}$ — which is what you get if you also add the assumption that $p_A$ = 50% precisely. And it is the background for Brennan’s (2011) result that $p_D$ is something like 1 in $10^{2,659}$ — which is what you get in an election the size of the 2004 US presidential election if you assume that $p_A$ is a plausible sounding vote share for a close election, such as 50.5%.

This is a remarkable discrepancy between two uses of the same model. It happens because the model produces a vote-share distribution with an extremely tall and narrow peak — especially for large elections. For a presidential sized election, it would be about 1,000 times taller and 1,000 times narrower than in my illustrative diagrams. Banzhaf configured this model to have the peak lining up exactly at the 50-50 split, leading to a very high estimate for a decisive vote. Brennan nudged the peak a small distance from the centre, but the peak is so slender that the curve’s height at the centre becomes microscopic.

Both versions are known to give poor estimates for the chance of a decisive vote. Banzhaf’s has been shown to be too high on empirical grounds (Gelman et al 2004). Brennan’s has been thoroughly embarrassed by the evidence: events his model said wouldn’t happen in the lifetime of the universe have already happened. For example, in 1985 control of the upper house for my home state of Victoria (Australia) with 2,461,708 voters came down to a single vote: any additional vote in Nunawading Provence would have determined the whole election in that party’s favour.

There are a number of flaws in the random voter model that cause such inaccurate predictions. A key one is that assumptions its practitioners are making determine where the peak goes, which directly determines whether the chance of a decisive vote is large or miniscule. Effectively Brennan is just assuming it is a close, but non-tied, election and saying that conditional on this there is very little chance it is tied. That obviously begs the question. If we slightly tweak the model to allow uncertainty about where the peak is (e.g. somewhere from 40% to 60%), then the dramatic results go away and you would get something in the vicinity of $\frac{1}{n}$. But then it is even better to avoid all need of the problematic modelling assumptions and directly use this probability distribution over vote share — or even just the simple probability that the underdog wins, as we’ve done in this piece.

I first developed this model in 2016 in the lead-up to the US presidential election, and wrote a near-final version of this essay explaining it in the wake of the 2020 election. I subsequently came across a superb paper by Zach Barnett (2020) that makes many of the same points (and more). Barnett’s paper is aimed at the broader conclusion that the expected moral value of voting often exceeds the costs to the voter, providing a moral case for voting along the lines that Parfit (1984) had advanced. As part of this, he too needed to bound the probability that one’s vote is decisive. His model for doing so was strikingly similar to mine (and we were both excited to discover the independent convergence). The key differences are:

1. Instead of making the probability a function of the underdog’s chance of winning, he makes the modelling assumption that the underdog will have a >10% chance of winning.

2. He makes an additional assumption that it is more likely the underdog wins by less than 10 points than that they win by more than 10 points.

By making these slightly stronger assumptions, he is able to reach a slightly stronger lower bound, which helps make the moral case for voting. Which one to use is something of a matter of taste (do you prefer unassailable assumptions or stronger conclusions?) and partly a matter of purpose: Barnett’s approach might be better for arguing that it is generally worth voting and mine for understanding the chance of a decisive vote itself.

References

J. R. Banzhaf, 1965, ‘Weighted Voting Doesn’t Work: A Mathematical Analysis’, Rutgers Law Review, 19 (1965), 317–43.

Zach Barnett, 2020, ‘Why you should vote to change the outcome’, Philosophy and Public Affairs, 48:422–446.

Jason Brennan, 2011, The Ethics of Voting (Princeton: Princeton University Press), 18–20.

Andrew Gelman, Jonathan N. Katz and Josef Bafumi, 2002, ‘Standard Voting Power Indexes Do Not Work: An Empirical Analysis’, B. J. Pol. Sci 34:657–674.

Andrew Gelman, Nate Silver and Aaron Edlin, 2010. ‘What is the probability your vote will make a difference?’, Economic Inquiry 50:321–326. 

Derek Parfit, 1984, Reasons and Persons (Oxford: Oxford University Press), 73–74.

27 March 2023